Воспроизведение реакций естественных нейронов как результат моделирования структурно-функциональных свойств мембраны и организации синаптического аппарата
А.В. Бахшиев, С.П. Романов
Моделирование информационных процессов в нервной системе требует воспроизведения соответствия как структуры связей между нейронами сети, так и принципов преобразования информационных (импульсных) потоков каждым нейроном. Известные математические модели нейрона либо не обладают необходимыми свойствами для решения такой задачи, либо требуют индивидуального подхода при моделировании каждого конкретного нейрона – составление уравнений для описания дендрита, синапса, составление уравнений связи, определение параметров моделей и т.п. Наиболее важным представляется разработка модели нейрона, функции и множество реакций которой будут определяться структурой ее дендритного и синаптического аппарата, причем изменение этой структуры не должно влиять на математическое описание либо модификацию параметров описания ее элементов. Нейронная сеть из таких нейронов будет представлять собой комплексную модель мембраны нервной ткани, взаимодействующей через модели химических или электрических синапсов, либо посредством тонического распространения потенциала по участкам мембраны. В работе предложена система дифференциальных уравнений, описывающая динамику преобразования импульсных потоков в естественном нейроне. Модель не требует настройки внутренних параметров в процессе функционирования. Свойства преобразования вход-выход нейронов определяют модификация структурной организации мембраны и синаптического аппарата и формируемые текущей активностью связи в сети. Разработана программная реализация предлагаемой модели нейрона и нейронных сетей. Преимуществом модели является возможность описания взаимодействия нейронов с произвольной структурой дендритного и синаптического аппарата. Возможна модификация моделей функциональных элементов нейрона (мембрана, синапс, низкопороговая зона) при условии сохранения интерфейсных соглашений о типе и диапазоне изменения входных и выходных данных этих элементов, либо выработки новых соглашений. Проведен ряд численных экспериментов, показавших возможность и методику описания в терминах структуры мембранного и синаптического аппаратов различных классов реакций нейронов на внешнее возбуждение.
Введение
Существующие математические модели нейронов либо очень просты, отражая лишь основные закономерности в обработке информации (такие как, например, алгебраическая суммация входных сигналов и изменение весов входов), присущие биологическому нейрону, либо рассматривают только отдельные этапы информационного преобразования сигналов и не дают целостного представления о процессах, происходящих в реальном объекте. Другая альтернатива – моделирование нейрона на уровне отдельных ионных каналов. Для решения задач исследования процессов обработки информационных (импульсных) потоков в естественных нейронных сетях такие модели представляются излишне подробными, предоставляющими эффективные средства описания химии протекающих процессов, но не комплексного описания принципов функционирования нейрона как системы обработки информации [1,2,3].
Перспективным представляется моделирование на уровне описания информационных преобразований импульсных потоков в нейроне, не спускаясь на уровень реализующих их физико-химических процессов, но и не абстрагируясь от понятия нейрона как объекта, осуществляющего нелинейные аналоговые преобразования потока импульсов [4,5]. Предлагаемая модель описывает нейронные структуры как единую нервную ткань - множество участков мембраны, взаимодействующих друг с другом посредством электрических и химических связей, группы которых формируют отдельные нейроны с их спецификой организации дендритного и синаптического аппарата.
Организация связей мембраны
В работе [6] подробно представлено описание исследуемой модели нейрона. В качестве функциональной основы модели нейрона принята схема (рис. 1) процессов преобразования импульсных потоков нейрона, предложенная в работах [7, 8].
Мембрана сомы и дендритов нейрона представляет собой набор моделей множества пар ионных механизмов, описывающих процессы деполяризации и гиперполяризации. Выходные сигналы блоков ионных механизмов представляют обобщенный аналоговый вклад в величину внутриклеточного потенциала от протекающих на мембране клетки процессов деполяризации и гиперполяризации.
Предлагается различать тип ионного механизма по знаку выходного сигнала. Положительное значение выхода характеризует деполяризующее влияние, отрицательное – гиперполяризующее, сумма которых изменяет потенциал в области генераторной зоны. Таким образом, суммарное значение выходных значений будет характеризовать величину вклада участка мембраны в суммарный внутриклеточный потенциал нейрона.
Модели нейронов взаимодействуют между собой посредством синаптических связей, функционально воспроизводящих процессы преобразования импульсов на синапсах с химической и электрической передачей возбуждения. Сигналы с синапсов изменяют деятельность ионных механизмов в сторону ослабления их функций, что моделирует изменение концентрации соответствующих ионов внутри клетки под влиянием внешнего воздействия. Следует отметить, что модели возбуждающих и тормозных синапсов идентичны друг другу, а различие в их воздействии на мембрану клетки определяется тем, к какому из ионных механизмов мембраны подключен каждый конкретный синапс.
В настоящей работе мы расширим область применения этой модели предложив несколько новых способов организации связей между участками мембраны (рис. 1).
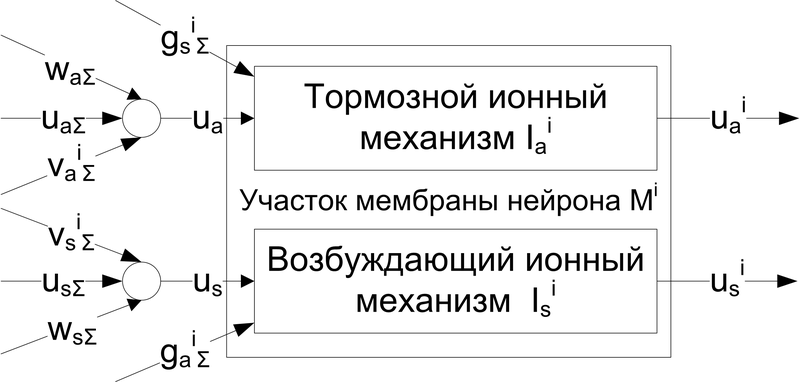
Рис. 1. Функциональная схема модели i-го участка мембраны нейрона Mi
Участок Mi мембраны состоит из пары механизмов – гиперполяризации и деполяризации. Выходом участка мембраны является пара значений гиперполяризации и деполяризации, определяющая их вклад в суммарный внутриклеточный потенциал. Каждый участок Mi может быть связан с другими участками Mj того же нейрона, принимая их пары значений.
Таким образом мы можем промоделировать ветвление дендритов нейрона.
Далее участок может быть связан аналогичным образом со множеством участков мембран других нейронов Mrn принимая их пары значений {van,vsn}.
Такие связи {van,vsn}, добавив к ним аналогичные обратные от Mi ко всем Mrn будем считать моделью электрических синапсов этих участков мембраны. При этом мы получаем возможность описывать как дендро-дендритные и дендро-соматические связи, так и электрический синапс.
В случае, когда заданный участок мембраны является последним в цепочке (окончание дендрита, участок сомы нейрона), в качестве пары значений гиперполяризации и деполяризации выступает пара фиксированных величин {Em}={Em+, Em-}, имитирующих некоторое начальное состояние ионных механизмов в покое.
Для моделирования механизмов взаимодействия потенциал-зависимых ионных каналов введем величины , которая может являться суммами выходов как , так и некоторых других участков мембраны того же нейрона . Единственным ограничением является обеспечение устойчивости таких связей.
Каждый химический синапс (далее под синапсом будем понимать синапс с химической передачей, если не указано иное) в модели описывает группу одноимённых синапсов естественного нейрона. Возбуждающими и тормозными входами нейрона являются входы множества моделей возбуждающих и тормозных синапсов для каждого из участков мембраны .
Результирующие значения влияния синапсов на механизмы гиперполяризации и деполяризации получаются в результате суммирования.
Ниже раскрывается математическое описание элементов модели нейрона, отличных от описанных ранее [6], и приводятся значения параметров моделей, используемые в дальнейших исследованиях.
Известно, что ионный канал можно представить в виде эквивалентной электрической схемы [9], которая имеет три основные характеристики – сопротивление , емкость и концентрацию ионов , поддерживаемую внутри клетки насосной функцией мембраны. Произведение характеризует инертность канала, т. е. определяет скорость восстановления нормальной концентрации ионов в клетке. Влияние синапса на ионный механизм заключается в потере эффективности насосной функции канала и в снижении концентрации ионов в клетке.
На рис. 2 (слева) представлена зависимость вклада синапса в изменение мембранного потенциала от соотношения сопротивлений канала синапса и постсинаптической мембраны. Можно видеть, что эффективный диапазон управления сопротивлением синапса лежит в диапазоне [0.1;10] сопротивлений мембраны.
Справа на рис.2 показана зависимость вклада в изменение потенциала от числа активных синапсов при соотношении Rs/Rm=10 (пунктир), и 1 (сплошная линия). По оси ординат на обоих графиках – нормированное изменение потенциала постсинаптической мембраны по отношению к его номинальному значению в покое.
Слева: зависимость эффективности от соотношения сопротивлений канала синапса и мембраны. Справа: зависимость эффективности от числа синапсов
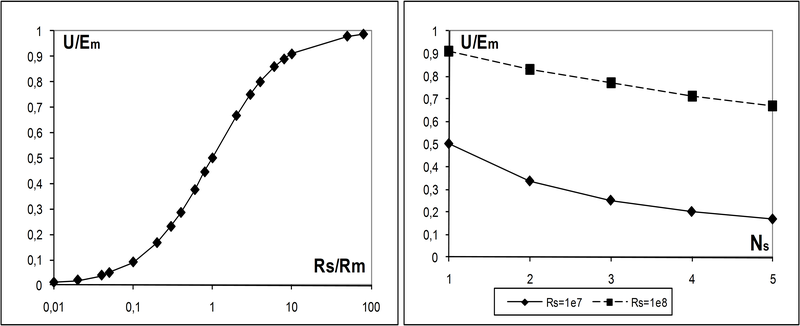
Рис.2. Актуальная эффективность модели химического синапса
Инерционные свойства модели ионного механизма предлагается описывать апериодическим звеном с логическим управлением постоянной времени. На рис. 3 представлена модель ионного механизма, соответствующая описанным выше свойствам.
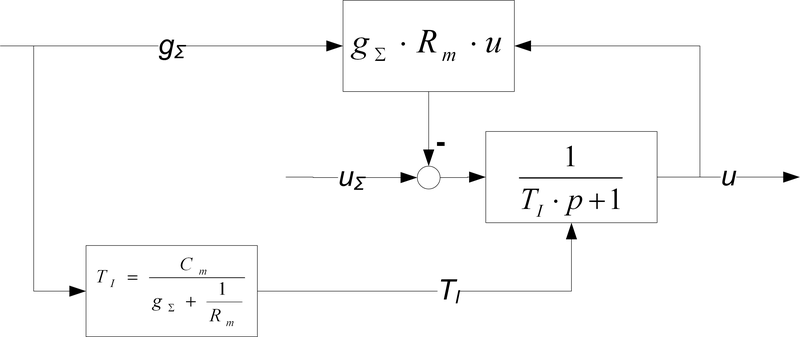
Рис. 3. Модель ионного механизма мембраны нейрона
Здесь - суммарная эффективность влияния синапсов на ионный механизм,
Rm - сопротивление мембраны в состоянии покоя (), и генерации импульса (),
Cm - емкость мембраны,
u∑ - ожидаемый вклад модели в величину внутриклеточного потенциала при отсутствии внешнего возбуждения: данная величина определяется активностью соседних участков мембраны,
u - реальный вклад модели в величину внутриклеточного потенциала.
Структурное описание моделей нейронов
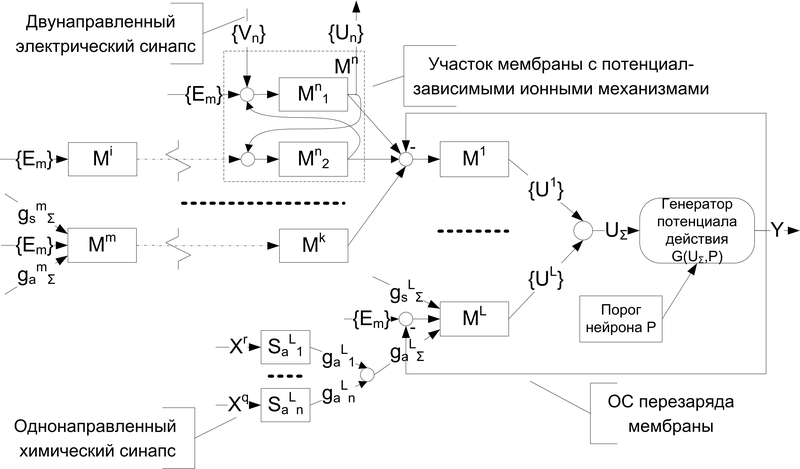
На рис.4 приведен общий вид структуры мембраны модели нейрона.
Рис. 4. Структурная схема мембраны нейрона
Телом нейрона условно будем считать те участки мембраны, которые охвачены обратной связью с генератора потенциала действия. Также следует отметить, что чем ближе участок мембраны расположен к генераторной зоне, тем эффективнее вклад его синапсов в общую картину возбуждения нейрона.
Таким образом, в терминах модели:
а) на дендритах осуществляется пространственная и временная суммация сигналов на значительных интервалах времени (малый вклад в возбуждение нейрона от каждого синапса), и накопление потенциала не зависит от разрядов нейрона;
б) на соме нейрона производится суммация сигналов на коротких интервалах времени (большой вклад в возбуждение нейрона от каждого синапса) и накапливаемый потенциал теряется при разрядах нейрона;
в) в низкопороговой зоне осуществляется формирование импульса при превышении порога генерации и сигнала перезаряда мембраны.
Параметры моделей
В таблице 1 приведены значения параметров моделей всех функциональных элементов нейрона. Эти значения использовались для всех экспериментов описываемых ниже. Значения параметров выбирались таким образом, чтобы наиболее наглядно продемонстрировать возможности качественного описания реакций естественных нейронов с различной организацией мембраны.
Таблица 1. Значения параметров модели нейрона
|
Синапс |
|
Постоянная времени выделения медиатора τs=0.001 c. Постоянная времени распада медиатора τd=0.01 с. Амплитуда входного сигнала Ey=1. Коэффициент влияния эффекта пресинаптического торможения ξ=2. Эквивалентное сопротивление канала (“вес” синапса) Rs=1∙108 Ом. |
|
Ионный механизм мембраны |
|
Эквивалентное сопротивление мембраны в состоянии покоя R0=107 Ом. Эквивалентное сопротивление в состоянии перезаряда RF=108 Ом. Эквивалентная емкость мембраны Cm=10-9 Ф. Начальные вклады {Em}={Em+, Em-} в мембранный потенциал ионных механизмов в состоянии покоя:
|
|
Генератор потенциала действия |
|
Порог нейрона P=0.001. Постоянная времени, определяющая инерцию генераторного механизма =0.005 с. Амплитуда выходного сигнала Ey=1. Коэффициент обратной связи F перезаряда мембраны для нейрона с числом участков мембраны сомы L (рис. 5):
Коэффициент F подбирался так, чтобы длительность импульса на выходе нейрона приблизительно равнялась 0.001с, соответствующей длительности импульсов, генерируемых биологическим нейроном. |
Исследования
В [6] были приведены структурные описания и наблюдаемые реакции крупных и малых нейронов, получаемых в модели путем изменения числа участков мембраны формирующих тело нейрона (M1-ML на рис.4). С ростом размера сомы при одинаковой стимуляции нейрона число импульсов в паттерне ответа нейрона уменьшается, а интервал между ними возрастает. На рис.5 слева демонстрируется зависимость средней частоты в спайке от числа импульсов в нем. Т.е. для графика 1 по оси абсцисс откладывается число импульсов в пачке Np. График 2 демонстрирует зависимость средней частоты следования спайков от числа участков сомы нейрона L. Частота вычислялась на фиксированном интервале времени, за который был принят интервал самого длинного паттерна.
На графике справа показана зависимость числа импульсов в спайке Np от числа участков мембраны сомы L.
Слева: зависимость средней частоты 1 – от числа Np импульсов в пачке; 2 – от числа участков сомы L
Справа: Зависимость среднего числа импульсов в пачке от числа участков сомы
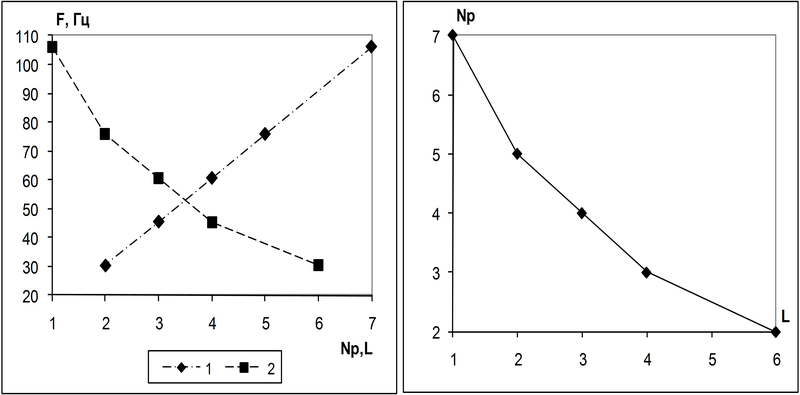
Рис. 5. Частота разрядов нейрона в зависимости от размера сомы
Далее рассмотрим изменения мембранного потенциала при различной организации дендритного и синаптического аппаратов (рис.6).
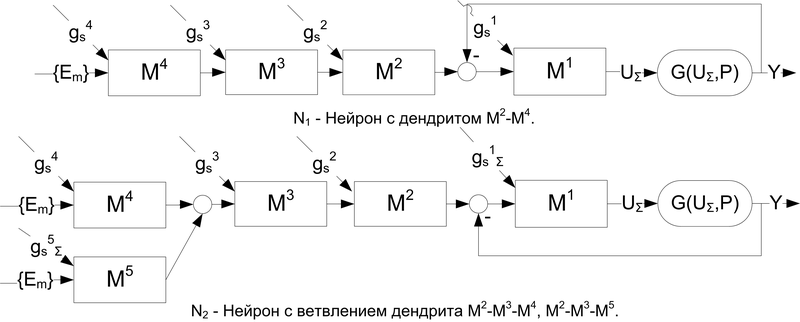
Рис.6. Ветвление дендритов
На рис. 7 (1) показаны изменения мембранного потенциала нейрона N1 на входе генераторной зоны при возбуждении по одному входу участка мембраны соответственно: a) – M4, b) – M3, c) – M2, d) – M1. Здесь наглядно демонстрируется временная задержка и затухание сигнала при распространении возбуждения по дендриту.
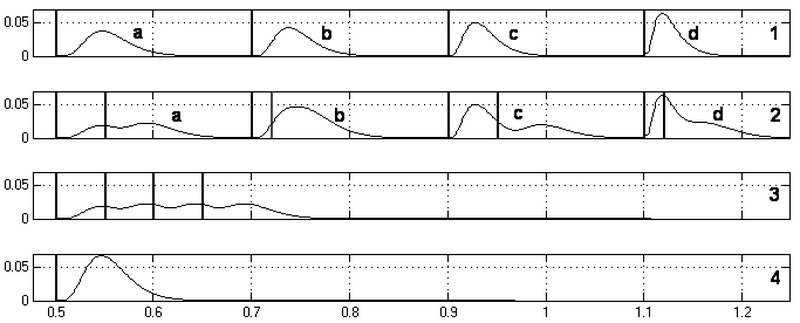
Рис.7. Потенциалы участков мембраны в местах ветвления дендритов при возбуждении по разным входам. По оси абсцисс время в секундах. Пояснения в тексте
На рис. 7 (2) показан пример пространственной и временной суммации влияний входных воздействий в местах ветвления дендритов нейрона N2. Здесь результирующее изменение мембранного потенциала получено при возбуждении в различные моменты времени одиночных синапсов на участках мембраны соответственно: a) – M4,M5, b) – M3,M5, c) – M2,M5, d) – M1,M5. На рис. 7 (3 и 4) демонстрируется пример соответственно чистой временной и пространственной суммации сигнала на 4 синапсах (участок мембраны M5). Здесь на (3) – M5 последовательно возбуждается одиночными импульсами по 4 входам; на (4) – импульс одновременно активирует все 4 входа вызывая усиленный всплеск деполяризации.
Другим частным случаем предлагаемой модели являются пейсмейкерные нейроны (рис.8). Частота реакций такого нейрона в отсутствии внешнего возбуждения может быть изменена (помимо величины порога нейрона P и величин эффективности ионных механизмов {Em} (см. таблицу 1) как модификацией размера сомы нейрона, так и глубины ОС перезаряда мембраны (пунктирная линия на рис.8).
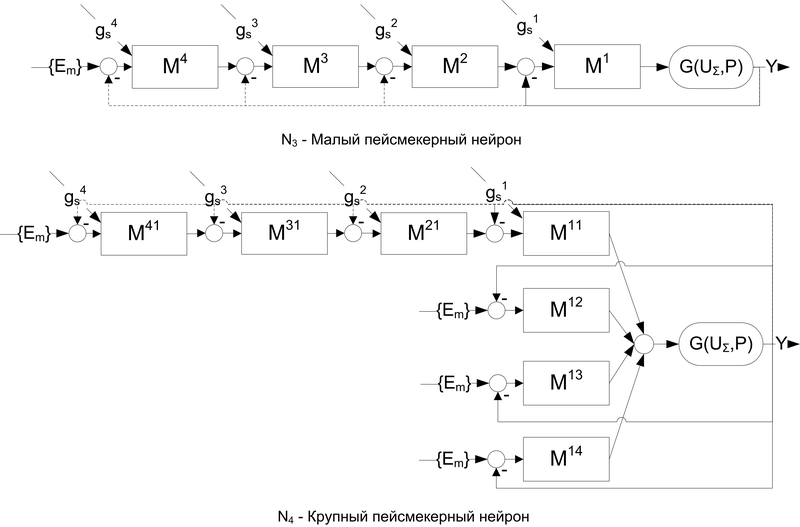
Рис. 8. Пейсмейкерные нейроны
На рис.9 представлены зависимости частоты периодических разрядов пейсмейкерных нейронов от числа параллельных включений участков мембраны в сому (1) и от глубины ОС (2).
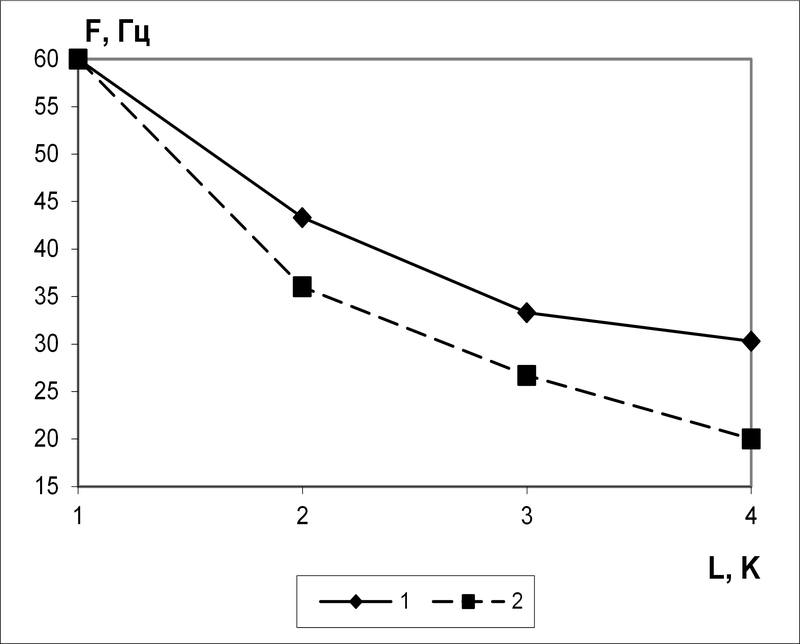
1 – частота разрядов нейрона от числа L параллельных включений участков мембраны в сому; 2 – частота разрядов от глубины ОС K
Рис. 9. Средняя частота реакций пейсмейкерных нейронов
На рис.10 показана простейшая модель нейрона, потенциал которого имеет множество устойчивых состояний. Эффект получен комбинацией положительных ОС с выходов ионных механизмов пары участков мембраны на их входы. Здесь для M21: , , где , выходы участка мембраны M22; для M22: , , где , выходы участка мембраны M21.
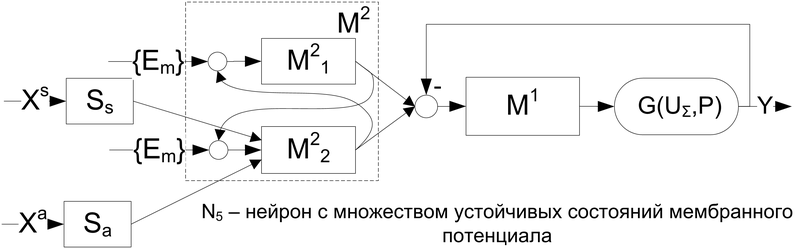
Рис. 10. Модель мембраны с несколькими стабильными состояниями
Ниже представлены реакции такой модели (рис.11). На графике 1 представлены входные сигналы. Первый импульс (слева) по возбуждающему входу, второй (справа) по тормозному. На графике 2 – мембранный потенциал на выходе потенциал-зависимого участка мембраны, график 3 – реакция на выходе генераторной зоны нейрона. По оси абсцисс – время в секундах.
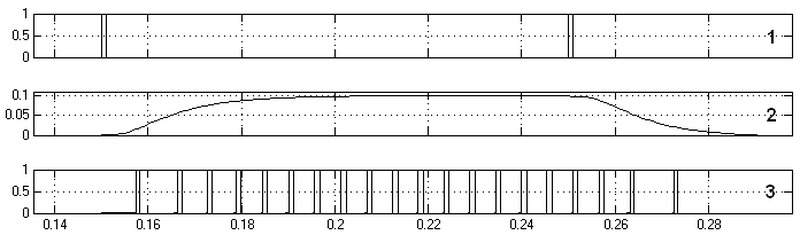
Рис. 11. Реакции нейрона со множеством устойчивых состояний мембранного потенциала - результаты
Подобные реакции наблюдаются у нейронов в простейших нервных системах, например, у первичнополостных червей, в частности, свободно живущей нематоды Caenorhabditis elegans [10].
На рис.12 демонстрируется два простейших варианта взаимодействия нейронов посредством электрического синапса. Отличие состоит в том, что синаптическая щель настолько узка, что электрическое возбуждение с пресинаптической мембраны непосредственно передаётся на постсинаптическую мембрану и формирует постсинаптический потенциал, распространяющийся далее по дендриту нейрона (следует отметить, что электрические синапсы встречаются у низших беспозвоночных).
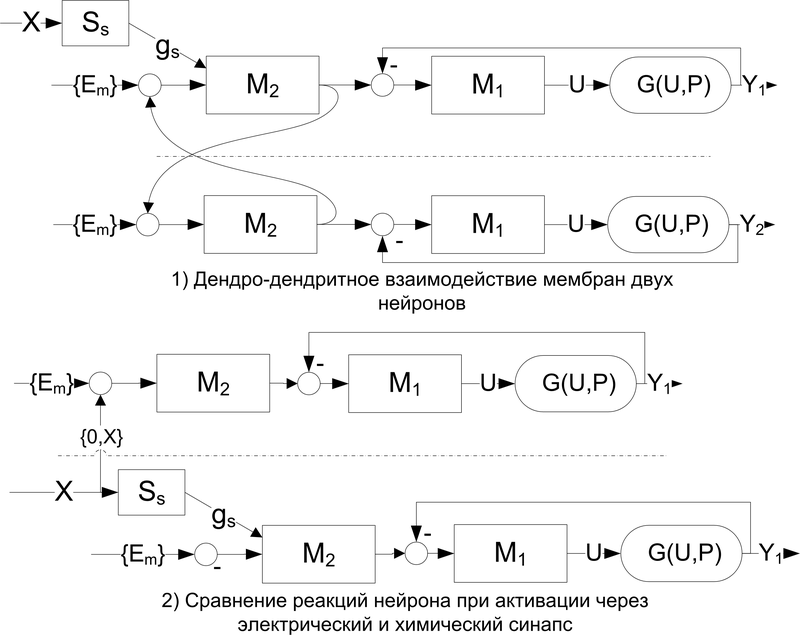
На рисунке вверху – показано дендро-дендритное взаимодействие двух нейронов, один из которых активируется электрическим синапсом.
Внизу – пара нейронов, активирующихся через электрический (вверху штриховой линии) и химический (внизу штриховой линии) синапсы.
Рис. 12. Взаимодействие нейронов посредством электрического синапса
Реакции моделей представлены на рис. 13. Здесь на всех графиках крайний левый импульс (начало импульса в момент времени 0.4с) – на возбуждающем входе соответствующего нейрона. Далее представлены импульсные реакции моделей нейронов и соответствующие мембранные потенциалы на входах генераторных зон нейронов. По оси абсцисс – время в секундах.
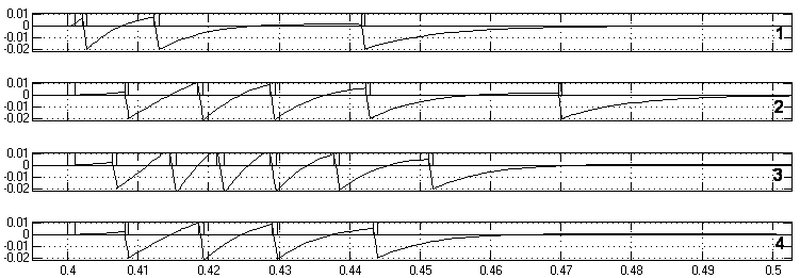
Реакции нейрона, возбуждаемого: 1 – электрическим синапсом; 2,3 – химическим синапсом; 4 – посредством дендритного взаимодействия с 3
Рис. 13. Сравнение реакций нейронов при возбуждении посредством электрической и химической синаптической передачи
На рис.14 представлена модель колебательной системы из 2х нейронов, которые отвечают в противофазе.
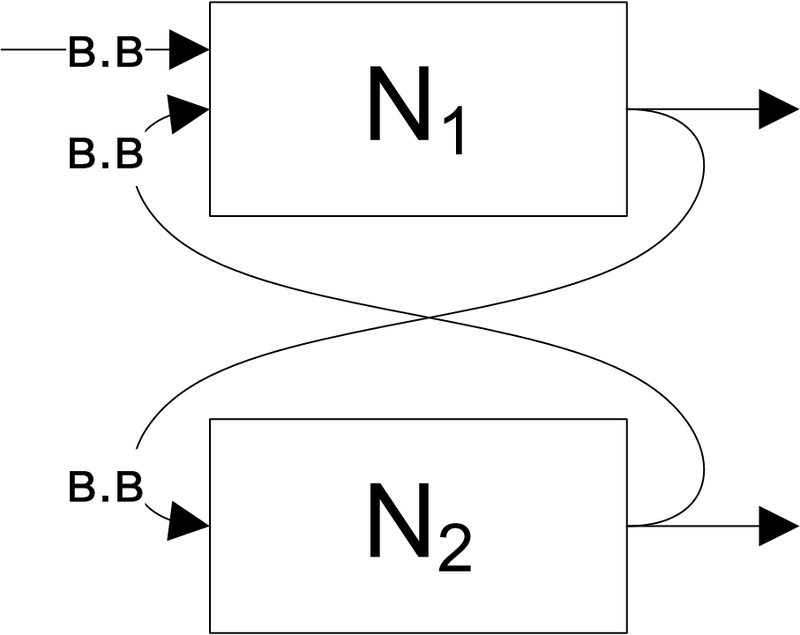
Рис. 14. Кольцевые структуры с положительными обратными связями
Временная диаграмма реакций модели представлена на рис.15. По оси абсцисс время в секундах, по оси ординат – амплитуды в условных единицах. На графиках 1 и 2 представлены разряды и мембранный потенциал нейронов N1 и N2 соответственно. Нейрон N1 разово запускается от внешнего генератора одиночным импульсом (на графике не показан).
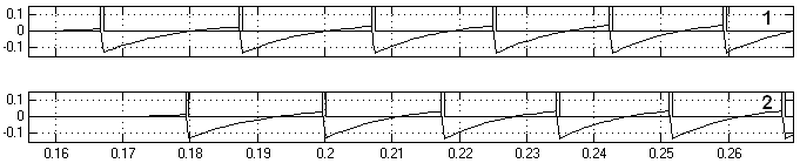
Рис. 15. Временная диаграмма реакций кольцевой структуры. Нейроны отвечают в противофазе
Заключение
Нервная система живых организмов решает два важных компонента унификации передачи и преобразования сигналов – это аналоговая форма обработки, позволяющая нейрону суммировать по пространству и интегрировать по времени входные воздействия, и импульсная передача сигналов с задержкой их распространения в проводящих трактах, использование которой позволяет решать задачи быстродействия и оптимальной регуляции функциями организма, анализируя изменения в окружающей среде.
В работе рассмотрены подходы к моделированию нейронов различного типа и механизмов их взаимодействия в составе сети как множества участков единой мембраны нервной ткани, на основе предложенной системы дифференциальных уравнений, описывающей процессы преобразования сигналов в естественном нейроне. Предложенное описание можно рассматривать в духе моделирования модульных нейронных сетей, имеющих выраженную морфологию совокупности нейронных модулей и связей [12].
Преимуществом нашей модели нейрона является возможность моделировать клетку как преобразователь импульсного (информационного) потока, с произвольной структурой синаптического и дендритного аппарата. Последовательное соединение участков мембраны моделирует длинный дендрит с функциями задержки и пространственного суммирования возбуждающих и тормозных сигналов, автоматически расставляя приоритеты синапсов в возбуждении нейрона – чем ближе участок мембраны в цепочке к низкопороговой зоне, тем эффективнее его синапсы возбуждают нейрон. Суммирование выходов нескольких участков мембраны описывает место ветвления дендритов и позволяет моделировать нейроны с большей инерцией в реакциях на внешние возбуждения. В зависимости от способа суммирования входных воздействий на участок мембраны и наличия положительных и отрицательных обратных связей с выхода этого участка на его входы (непосредственных или опосредованно через другие участки) становится возможным описывать мембрану с несколькими стабильными состояниями мембранного потенциала, а также моделировать взаимодействие посредством электрического синапса и другие эффекты тонического распространения потенциала по мембране.
Проведенные исследования показали, что разработанные модели нейронов адекватно представляют многие процессы преобразования информации, свойственные естественным прототипам, в том числе такие как пластичность и эффект пресинаптического торможения. Кроме того, в отличие от нейросетевых технологий, формируется новая вычислительная среда с импульсной передачей сигналов и широкими возможностями модуляции связей в нейронной структуре самими входными воздействиями, функционально изменяя её топологию для формирования соответствующего обстановке выхода на исполнительные органы. В отличие от однородных нейронных структур, обучение которых происходит при разомкнутом контуре между выходом сети и её входом, т.е. в процессе обучения изменением весов входов формируется структура сети, ставящая в определённое соответствие матрицы входных сигналов с состоянием её выходов, в предлагаемом подходе к конструированию нейрона достаточная и необходимая нейронная структура может формироваться только в режиме её функционирования в замкнутом контуре с объектом управления.
Следующим этапом является анализ естественных нейронных структур обработки зрительной информации по выделению существенных признаков и формирование нейронных структур управления движителем с разработкой моделей замкнутых контуров управления по принципу “глаз-рука”.
В дальнейшем надеемся на возможность разработки нейронных структур анализа сенсорной информации и управления движением робототехнических систем, реализующих все этапы преобразования информации от сенсоров до эффекторов свойственных естественным прототипам; определение принципов построения нейронной иерархичной системы управления объектами, с последовательным наращиванием функциональности такой системы от уровня к уровню.
В перспективе планируется построение модели автономного мобильного робота, система управления которого на нейронной сети с использованием рассмотренных аналогов нейронов должна обеспечить поддержание собственного функционирования и поиск предустановленных и задаваемых целей в физической среде с меняющейся обстановкой.
Литература
1. Романов С.П. Структурное обоснование функции нервной системы как автоматического регулятора. - Нейрокомпьютеры: разработка, применение. 2006, № 7, с. 54-63.
2. Романов С.П. Нейросистемы и современные вычислительные среды. - Нейрокомпьютеры: разработка, применение. 2007, № 6, с. 96-104.
3. Hodgkin A.L., Huxley A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve. – J. Physiology. 1952, 117, pp. 500-544.
4. Романов С.П., Бахшиев А.В. Математическая модель биологического нейрона. - Моделирование неравновесных систем - 2000: Материалы III Всероссийского семинара, Красноярск, 20-22 октября 2000 г. - Красноярск: ИПЦ КГТУ, 2000. 307 с.
5. Бахшиев А.В. Компьютерное моделирование естественных нейронных сетей. - Материалы XIV научно-технической конференции “Экстремальная робототехника” СПб.: Астерион, 2004.
6. Бахшиев А. В., Романов С. П. Математическое моделирование процессов преобразования импульсных потоков в биологическом нейроне // Нейрокомпьютеры: разработка, применение. №3, стр. 71-80, 2009.
7. Романов С.П. Модель нейрона. - Некоторые проблемы биологической кибернетики. – Л.: Наука, 1972, с. 276-282.
8. Романов С.П. Моделирование свойств ионного канала и исследование его роли в формировании импульсной активности нейрона. – Нейрофизиология, 1989, Т. 21, №3, с. 379-389.
9. Экклс Дж. Физиология синапсов. Москва: Мир. 1966. 395 с.
10. Lockery S.R, Goodman M.B. The quest for action potentials in C. elegans neurons hits a plateau // Nature Neuroscience volume 12, number 4, 377-378 (April 2009).
12. Дорогов А.Ю., Алексеев А.А. Категории ядерных нейронных сетей //Всерос. науч.-техн. конф.«Нейроинформатика-99» г.Москва 20-22 января 1999г. Сб.науч.тр.Часть 1.-М.: 1999.-С.55-64.